Model Binding

Model Binding in Razor Pages is the process that takes values from HTTP requests and maps them to handler method parameters or PageModel properties. Model binding reduces the need for the developer to manually extract values from the request and then assign them, one by one, to variables or properties for later processing. This work is repetitive, tedious and error prone, mainly because request values are usually only exposed via string-based indexes.

The Problem

To illustrate the role that model binding plays, create a new Razor page with a PageModel and name it ModelBinding.cshtml. Change the code in the content page to the following:

@page 
@model ModelBindingModel
@{
}

<h3>@ViewData["confirmation"]</h3>
<form class="form-horizontal" method="post">
    <div class="form-group">
        <label for="Name" class="col-sm-2 control-label">Name</label>
        <div class="col-sm-10">
            <input type="text" class="form-control" name="Name">
        </div>
    </div>
    <div class="form-group">
        <label for="Email" class="col-sm-2 control-label">Email</label>
        <div class="col-sm-10">
            <input type="text" class="form-control" name="Email">
        </div>
    </div>
    <div class="form-group">
        <div class="col-sm-offset-2 col-sm-10">
            <button type="submit" class="btn btn-default">Register</button>
        </div>
    </div>
</form>

It represents a standard HTML form accepting a name and a email address (such as might be used to capture requests for information, for example), with a confirmation message at the top of the page. When the form is completed and submitted, the values are sent in the request body in name/value pairs, where the "name" represents the name attribute of the input, and the value is what was supplied by the user. You can see this in the Network tab of your preferred browser if it supports developer tools:

Add the following handler method code to the PageModel class in ModelBinding.cshtml.cs:

public void OnPost()
{
    var name = Request.Form["Name"];
    var email = Request.Form["Email"];
    ViewData["confirmation"] = $"{name}, information will be sent to {email}";
}

This represents the traditional way that values in server-side code are processed in many web frameworks. The appropriate Request collection is accessed by string-based index and then values from the collection are assigned to local variables for further processing.

Launch the page in a browser and enter some values into the form. Then submit it and you should see those values included in the confirmation message:

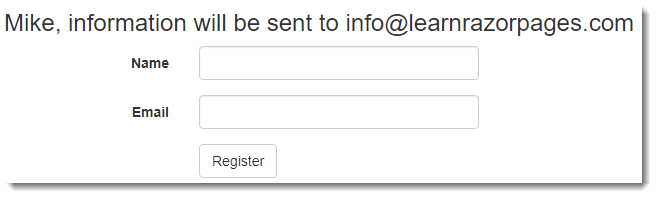
This approach is sustainable for small forms, but if you are dealing with large forms, such as one representing an order for multiple items complete with shipping details, for example, the assignment code can become very tedious. And, because development tools provide no code-completion or Intellisense support for string indices, it is fairly easy to mistype Request.Form["Email"] as Request.Form["Emial"], thereby introducing a subtle but damaging bug that may be difficult to track down among 30 or 40 other form fields.

Binding Posted Form Values To Handler Method Parameters

Razor Pages provides two approaches to leveraging model binding. The first approach involves adding parameters to the handler method. The parameters are named after the form fields, and given an appropriate type for the expected data. To see this approach in action, remove the assignment code in the OnPost handler method and add two parameters to the method:

public void OnPost(string name, string email)
{
     ViewData["confirmation"] = $"{name}, information will be sent to {email}";
}

When the form is posted, the Razor Pages framework calls the OnPost method and sees that it has two parameters. It extracts posted form values that match the names of the parameters and automatically assigns the values from the form to the parameters if the value can be converted to the type represented by the parameter. There is no need for any assignment code.

Binding Posted Form Values to PageModel Properties

The previous approach is suitable when the values are not needed outside of the handler method to which the parameters belong. The second approach is more suitable if you need to access the values outside of the handler method (for display on the page or binding to tag helpers, for example), or if you prefer to work in a strongly typed manner within the Razor content page. This approach involves adding public properties to the PageModel (or to a @functions block if you don't want to use the PageModel approach) and then decorating them with the BindProperty attribute. To try this out, alter the PageModel code as follows:

public class ModelBindingModel : PageModel
{
    [BindProperty]
    public string Name { get; set; }
    [BindProperty]
    public string Email { get; set; }
    public void OnGet()
    {
    }

    public void OnPost()
    {
        ViewData["confirmation"] = $"{Name}, information will be sent to {Email}";
    }
}

From version 2.1 of ASP.NET Core, you can add the new [BindProperties] attribute to the PageModel class rather than applying [BindProperty] to individual properties, which results in all the public properties in the PageModel taking part in model binding:

[BindProperties]
public class ModelBindingModel : PageModel
{
    public string Name { get; set; }
    public string Email { get; set; }
    
    public void OnGet()
    {
    }

    public void OnPost()
    {
        ViewData["confirmation"] = $"{Name}, information will be sent to {Email}";
    }
}

When doing this, take care to note the advice about preventing over-posting attacks below.

Note that the case of the variables in the format string has altered to refer to the public property names. Model binding itself is not case sensitive. It performs case-insensitive matches between the names of incoming values and the names or parameters or properties that it attempts to bind the values to. Now when you run the page, the result is exactly the same as before:

Binding Data From GET Requests

The same options apply if you want to bind data from GET requests (which is appended to the URL as a query string). Binding to handler method parameters is automatic and requires no additional configuration. However, by default, only values that form part of a POST request are considered for model binding when you use the BindProperty attribute. The BindProperty attribute has a property called SupportsGet, which is false by default. You have to set this to true to opt in to model binding to PageModel properties on GET requests:

public class ModelBindingModel : PageModel
{
    [BindProperty(SupportsGet = true)]
    public string Email { get; set; }
    [BindProperty(SupportsGet = true)]
    public string Password { get; set; }
    public void OnGet()
    {
        ViewData["welcome"] = $"Welcome {Email}";
    }
}

Binding Route Data

So far the examples have featured how model binding works with form values. It also works with Route Data, which is part of the routing system that Razor Pages uses. To test this, alter the code in ModelBinding.cshtml as follows:

@page "{id}"
@model ModelBindingModel
@{
}

<h3>Id = @ViewData["id"]</h3>

A route parameter named id has been added and the content of the h3 heading has been altered to print the value of a ViewData entry named id.

Next, remove the public properties from the PageModel and add a parameter named id of type int to the OnGet handler method, and in the body of the method, assign its value to ViewData:

public class ModelBindingModel : PageModel
{
    public void OnGet(int id)
    {
        ViewData["id"] = id;
    }
}

Once again, model binding takes care of assigning the value in the route to the handler method parameter. This also works for public properties on the PageModel in exactly the same way as for form values:

public class ModelBindingModel : PageModel
{
    [BindProperty(SupportsGet= true )]
    public int Id { get; set; }

    public void OnGet()
    {
        ViewData["id"] = Id;
    }

    public void OnPost()
    {
            
    }
}

Binding Complex Objects

Up to this point, you have seen how to use model binding to populate simple properties. As the number of form fields grows, the PageModel class will start to creak with either a long list of properties, all decorated with the BindProperty attribute, or a large number of parameters applied to a handler method. Fortunately model binding also works with complex objects. So the properties to be bound can be wrapped in an object that can be exposed as a property of the PageModel or a parameter for the handler method. Here's a class named Login that represents the form fields from the previous examples:

public class Login
{
    public string Email { get; set; }
    public string Password { get; set; }
}

Now this can be added as a property on the PageModel class:

public class ModelBindingModel : PageModel
{
    [BindProperty]
    public Login Login { get; set; }
    public void OnGet()
    {
    }

    public void OnPost()
    {
        ViewData["welcome"] = $"Welcome {Login.Email}";
    }
}

Or it can be applied as a parameter to the OnPost method depending on your usage needs:

public class ModelBindingModel : PageModel
{
    public void OnGet()
    {
    }

    public void OnPost(Login Login)
    {
        ViewData["welcome"] = $"Welcome {Login.Email}";
    }
}

The form field names have to be altered to reflect the fact that the property has changed:

<input type="text" class="form-control" name="Login.Email">

Binding Complex Objects In A Get Request

Model binding in GET requests works with complex objects decorated with the BindProperty attribute as long as the SupportsGet parameter is set to true, just as with simple types. Or you can add the type as a handler method parameter:

public class ModelBindingModel : PageModel
{
    public void OnGet(Login login)
    {
        ViewData["welcome"] = $"Welcome {Login.Email}";
    }
}

Binding Simple Collections

The next code example shows a form where the user is allowed to select more than one option. In this case, the user is invited to specify which film categories they like:

<form class="form-horizontal" method="post">
    <div class="form-group">
        <label for="CategoryId" class="col-sm-2 control-label">Which types of film do you like? (Tick all that apply)</label>
        <div class="col-sm-10">
            <input type="checkbox" name="CategoryId" value="1"> Factual<br />
            <input type="checkbox" name="CategoryId" value="2"> Horror<br />
            <input type="checkbox" name="CategoryId" value="3"> Historical<br />
            <input type="checkbox" name="CategoryId" value="4"> SciFi<br />
            <input type="checkbox" name="CategoryId" value="5"> Comedy<br />
            <input type="checkbox" name="CategoryId" value="6"> Fantasy<br />
        </div>
    </div>
    <div class="form-group">
        <div class="col-sm-offset-2 col-sm-10">
            <button type="submit" class="btn btn-default">Submit</button>
        </div>
    </div>
</form>

The form includes multiple checkboxes, each with the same name attribute value: CategoryId. When the form is submitted, the posted values look something like this (depending on the selection made):

CategoryId=1&CategoryId=3&CategoryId=6

ASP.NET Core will take those values and transform them into a StringValues type, which represents zero/null, one, or many strings. This can be converted by the model binder to an array of any type that the values can be converted to - strings or integers will work in this example. The code for binding to a handler method parameter and passing the posted values to ViewData looks like this:

public void OnPost(int[] categoryId)
{
    ViewData["categoryId"] = categoryId;
}

If there are no values posted, categoryId will be null as will ViewData["categoryId"]. Therefore you must test for null (as well as casting to the relevant type):

@if (ViewData["categoryId"] != null)
{
<h3>You selected the following categories: @string.Join(",", (int[])ViewData["categoryId"])</h3>
}

If you choose to bind to a PageModel property, you can initiate the collection as part of its declaration:

public class ModelBindingModel : PageModel
{
    [BindProperty]
    public int[] CategoryId { get; set; } = new int[0];

    public void OnPost()
    {
            
    }
}

Then you can use Any() to check whether the collection has been populated:

@if (Model.CategoryId.Any())
{
<h3>You selected the following categories: @string.Join(",", Model.CategoryId)</h3>
}

Binding Complex Collections

The model binder also supports binding to collections of complex objects. The following class represents a contact:

public class Contact
{
    public int ContactId { get; set; }
    public string FirstName { get; set; }
    public string LastName { get; set; }
    public string Email { get; set; }
}

Here is a form that enables a user to submit multiple contacts in one go:

<form class="form-horizontal" method="post">
    <table class="table table-striped">
            <tr>
                <th>First Name</th>
                <th>Last Name</th>
                <th>Email</th>
            </tr>
        @for (var i = 0; i < 5; i++)
        {
            <tr>
                <td>
                    <input type="text" name="[@i].FirstName" />
                </td>
                <td>
                    <input type="text" name="[@i].LastName" />
                </td>
                <td>
                    <input type="text" name="[@i].Email" />
                </td>
            </tr>
        }
    </table>
    <div class="form-group">
        <div class="col-sm-offset-2 col-sm-10">
            <button type="submit" class="btn btn-default">Submit</button>
        </div>
    </div>
</form>

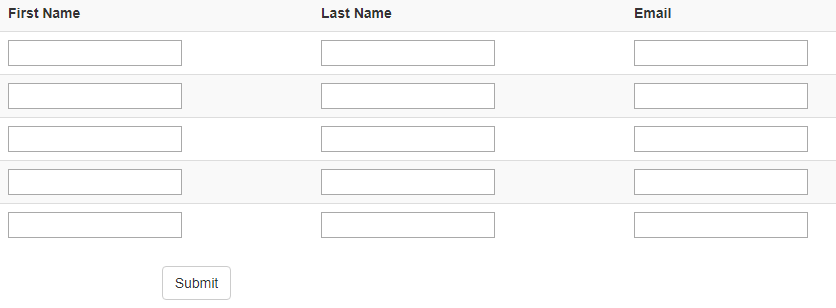
The model binder will bind the posted values to a collection of Contact objects, which is usually represented by a List<T>. This can be a property of the PageModel:

[BindProperty]
public List<Contact> Contacts { get; set; }

Or it can be a handler method parameter:

public void OnPost(List<Contact> contacts)
{
    // process the contacts
}

This approach to complex object binding makes use of a sequential index. The index must start at 0, and it must be sequential, as its name suggests. There must be no gaps. The index is placed in square brackets and added to the form field's name attribute e.g [0].FirstName. The code below shows the generated HTML for the first 2 rows in the form:

<tr>
    <td>
        <input type="text" name="[0].FirstName" />
    </td>
    <td>
        <input type="text" name="[0].LastName" />
    </td>
    <td>
        <input type="text" name="[0].Email" />
    </td>
</tr>
<tr>
    <td>
        <input type="text" name="[1].FirstName" />
    </td>
    <td>
        <input type="text" name="[1].LastName" />
    </td>
    <td>
        <input type="text" name="[1].Email" />
    </td>
</tr>

In this example, for format that is used for the form field names is [index].propertyname. The process also works with parametername[index].propertyname if you prefer e.g.:

@for (var i = 0; i < 5; i++)
{
    <tr>
        <td>
            <input type="text" name="Contacts[@i].FirstName" />
        </td>
        <td>
            <input type="text" name="Contacts[@i].LastName" />
        </td>
        <td>
            <input type="text" name="Contacts[@i].Email" />
        </td>
    </tr>
}

When the form is submitted, a collection of five (in this example) Contact objects is instantiated and populated with the posted values. If the user only provides values for the first three contacts, the final two will have their properties set to the default for the type - null for strings.

The same approach works when you bind to a PageModel property. However, you can also use the asp-for attribute of an input tag helper:

@for (var i = 0; i < 5; i++)
{
    <tr>
        <td>
            <input type="text" asp-for="Contacts[i].FirstName" />
        </td>
        <td>
            <input type="text" asp-for="Contacts[i].LastName" />
        </td>
        <td>
            <input type="text" asp-for="Contacts[i].Email" />
        </td>
    </tr>
}

public class ModelBindingModel : PageModel
{
    [BindProperty]
    public List<Contact> Contacts { get; set; } 


    public void OnPost()
    {
        // process the contacts
    }
}

You can also use an explicit index. This approach requires an additional hidden field for each item, named [property].Index (the explicit index). The index can be any value that uniquely identifies a data item. This approach is more suited to forms designed for editing existing values, where the primary key of each item is often used as the index value.

In this example, ContactId - the key value for the Contact entity - is used as the index value:

<form method="post">
    <table class="table">
        @foreach (var contact in Model.Contacts)
        {
            <tr>
                <td>
                    <input type="hidden" name="Contacts.Index" value="@contact.ContactId" />
                    <input type="hidden" name="Contacts[@contact.ContactId].ContactId" value="@contact.ContactId" />
                    @contact.ContactId
                </td>
                <td><input name="Contacts[@contact.ContactId].FirstName" value="@contact.FirstName" /></td>
                <td><input name="Contacts[@contact.ContactId].LastName" value="@contact.LastName" /></td>
                <td><input name="Contacts[@contact.ContactId].Email" value="@contact.Email" /></td>
            </tr>
        }
    </table>
    <button>Update</button>
</form>

This is how one row of data might render, given some actual values:

<tr>
    <td>
        <input type="hidden" name="Contacts.Index" value="43907" />
        <input type="hidden" name="Contacts[43907].ContactId" value="43907" />
        43907
    </td>
    <td><input name="Contacts[43907].FirstName" value="Penny" /></td>
    <td><input name="Contacts[43907].LastName" value="Farthing" /></td>
    <td><input name="Contacts[43907].Email" value="[email protected]" /></td>
</tr>

The model binders uses the Contacts.Index field value to group other values.

Binding Related Collections to a Complex Object

Sometimes you may want to create a form that enables the creation of a parent object along with one or more items belonging to a collection property of the parent. One of the easier examples of this to understand is an order and its items. The following simple model illustrates this relationship:

public class Order
{
    public int OrderId { get; set; }
    public string Customer { get; set; }
    public List<OrderItem> OrderItems { get; set; }
}

public class OrderItem
{
    public int OrderItemId { get; set; }
    public string Item { get; set; }
    public decimal Price { get; set; }
}

Here's the PageModel for a Create page:

@page
@model CreateModel
@{
}

<form method="post">
    <input asp-for="Order.Customer" /><br />
    <input asp-for="Order.OrderItems[0].Item" /><br>
    <input asp-for="Order.OrderItems[0].Price" /><br>
    <input type="submit"/>
</form>

Finally, the PageModel with an Order property decorated with the [BindProperty] attribute:

public class CreateModel : PageModel
{
    [BindProperty]
    public Order Order { get; set; }


    public void OnPost()
    {

    }
}

The indexer is applied to the OrderItems property of the Order. When the form is posted back, the model binder will create an Order object, and an OrderItem object, which will be assigned to the OrderItems collection of the Order:

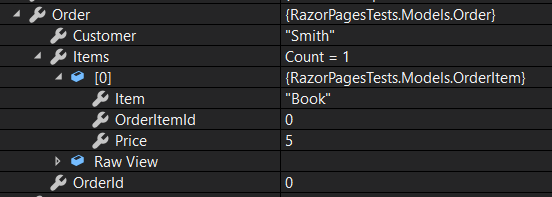
Binding to Arbitrary Keys

When binding posted values, ASP.NET Core matches the names of the form or query string keys in the request to parameter names or the names of public properties decorated with the BindProperty attribute. A form field with a name attribute of person.firstname will be bound to Person.FirstName. Sometimes, you might want to override the default matching. This is possible by specifying a value for the Name property of the BindProperty attribute as in the following code example:

public class Person
{
    [BindProperty(Name="first-name")]
    public string FirstName { get; set; }
    public string LastName { get; set; }
}

In a PageModel, the BindProperty attribute is applied to an instance of the Person class:

[BindProperty]
public Person Person { get; set; }

And in the form, the name attributes on the inputs are as follows:

<form method="post">
    First Name: <input name="first-name"/><br>
    Last Name: <input name="person.lastname" /><br>
    <button>Submit</button>
</form>

Preventing Overposting or Mass Assignment Attacks

When you add the BindProperty attribute to a class, all properties in that class are automatically included in model binding. That may not be what is needed, particularly when working with Entity Framework model classes.

For example, you might choose to have an IsDeleted property on your entities to allow "soft deletes" (i.e. a flag that specifies the status of a record rather than the permanent - and irrevocable - removal of the record from the database). Only admins are allowed to set this property so you don't include an IsDeleted field in the edit form for normal users:

<form class="form-horizontal" method="post">
    <input type="hidden" asp-for="ContactId">
    <div class="form-group">
        <label asp-for="Name" class="col-sm-2 control-label"></label>
        <div class="col-sm-10">
            <input type="text" class="form-control" asp-for="Name">
        </div>
    </div>
    <div class="form-group">
        <label asp-for="Email" class="col-sm-2 control-label"></label>
        <div class="col-sm-10">
            <input type="text" class="form-control" asp-for="Email">
        </div>
    </div>
    <div class="form-group">
        <div class="col-sm-offset-2 col-sm-10">
            <button type="submit" class="btn btn-default">Edit</button>
        </div>
    </div>
</form>

However, it is trivial for a reasonably competent HTML-savvy user to manipulate the form (using the standard browser developer tools, for example) to include an IsDeleted property and to submit that to the server. The value will be processed as part of a legitimate edit operation. This is known as a mass assignment or an over posting attack.

For this reason, you are advised to be careful when using model binding with complex types. If they include properties that should not be set by an unauthorised user, you should only include the properties that can be set, either as individual properties on the PageModel, or wrapped in a ViewModel class.

Further Reading

• Implementing a Custom Model Binder in Razor Pages